Логические операторы
Часто выражения, содержащиеся в операторе if, состоят из нескольких простых выражений, объединенных логическими операторами. Они описывают логические операции: и (конъюнкция), или (дизъюнкция), нет (отрицание) .

Давайте посмотрим, как работают эти операции. Логическая операция и (обозначается в C: && ) . Пусть E1 и E2 – – два логических выражения. Каждое из них может быть истинным (T) или ложным (F). Все возможные комбинации значений описаны в таблице истинности для E1 && E2:
Результат операции && есть True (1) тогда и только тогда, когда оба выражения E1 и E2 aимеют значение True. Операция также называется «логическим умножением»
Логическая операция или (обозначается в C: || ). Пусть E1 и E2 – два логических выражения. Каждое из них может быть истинным (T) или ложным (F). Все возможные комбинации значений описаны в таблице истинности для E1 || E2:
Результат операции || есть True (1) тогда и только тогда, когда оба выражения E1 и E2 имеет значение True. Операцию также называют «логическим сложением»


Логическое отрицание (обозначается в C: ! ). Пусть E логическое выражение. Оно может быть истинным или ложным. Соответственно !E будет иметь обратное значение:
Операции &&, || и ! имеют различный приоритет. Наивысший приоритет у унарной операции !, следует && а самым низким приоритетом обладает ||.
Использование логических операций в условных операторах
Пример 6.2
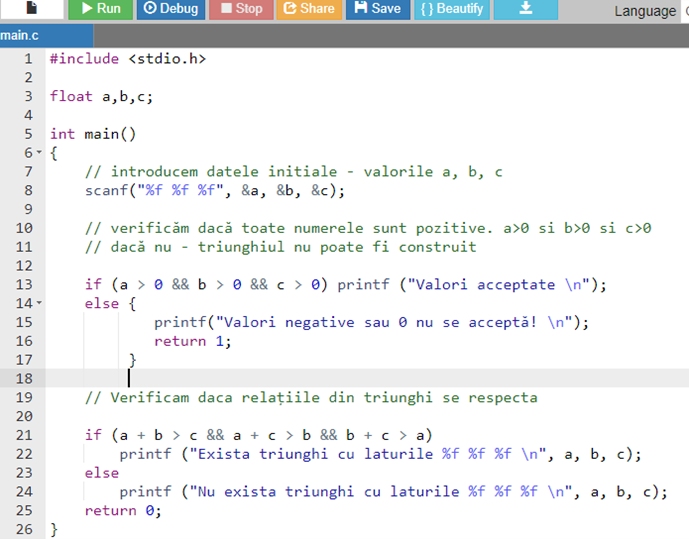
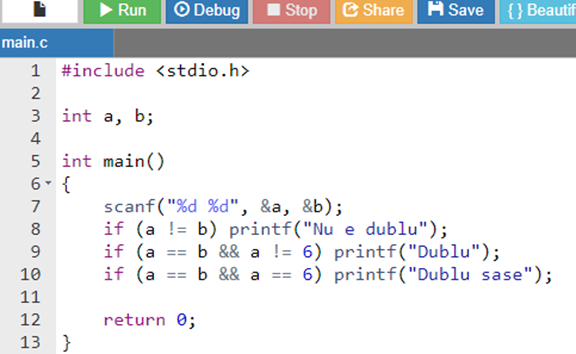
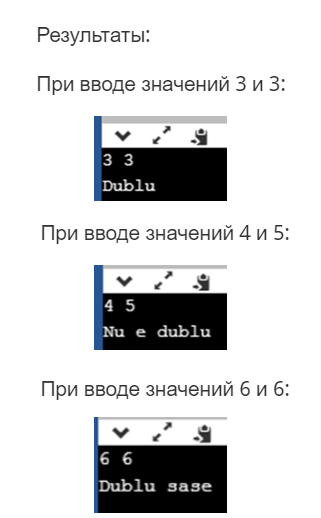
Пусть a и b – значения на верхних сторонах двух игральных костей после броска. Считается, что был выброшен дубль, если оба значения равны. Считается, что было выброшено дубль шесть если обе верхние стороны имеют значение 6. Напиши программу которая будет считывать значения a и b, и будет отображать одно из сообщений
- Nu e dublu – если значения a и b различны;
- Dublu – если значения a и b равны, но отличны от 6;
- Dublu șase – оба значения a и b равны 6;

Анализ: для решения необходимо только сравнить между собой значения a и b, и, в случае равенства- с константой 6:
Если (a != b) вывести сообщение ”Nu e dublu”
Если (a == b && a != 6) вывести сообщение ”Dublu”
Если (a == b && a == 6) вывести сообщение ”Dublu șase”
Поскольку описанные ситуации не могут происходить одновременно, будет выполнен только тот из операторов, для которого описанное условие истинно!
У нас есть метод решения, мы можем написать программу!
Пример 6.3
Задача: пусть мы должны написать программу, которая определит, могут ли три положительных числа a, b, c соответствовать длинам сторон произвольного треугольника.
Решение: мы знаем, что для того, чтобы три положительных чисел a,b,c, соответствовали длинам сторон треугольника сумма любых двух из них должна быть больше, чем третье. Другими словами, если a+b>c и a+c>b и b+c>a тогда a,b,c могут быть сторонами треугольника, в противном случае – нет.
У нас есть метод решения, мы можем написать программу!