Ce este sortarea prin selecție
Sortarea prin selecție este expresia modului firesc de ordonare a obiectelor, folosit în activitățile cotidiene. Fie că dorești să ordonezi cărțile de pe un raft după înălțime, astfel încât cele mai înalte cărți să se afle în partea din dreapta a raftului. Nu vei compara înălțimile pentru fiecare pereche de cărți. Vizual, vei căuta cartea cu cea mai mare înălțime și o vei schimba cu locul cu cea mai din dreapta carte de pe raft.
Apoi, vei repeta același procedeu pentru cărțile neordonate încă, ignorând cartea, care este deja la locul său. Din nou, vei căuta cartea cu cea mai mare înălțime, iar după ce o vei găsi, o vei schimba cu locul cu ultima (cea mai din dreapta) dintre cărțile încă neordonate!
Acum, în partea din dreapta a raftului vei avea deja două cărți cu cele mai mari înălțimi, aranjate corect.
Repeți procedeul încă odată. Cea de-a treia, cea mai înaltă carte, ajunge la locul său, după ce o găsești printre cărțile neordonate încă și o schimbi cu locul cu ultima dintre cărțile neordonate…
Dacă pe raft sunt n cărți, procedeul se va repeta de n-1 ori până când toate cărțile vor ajunge fiecare la locul său. Ultima carte se va așeza ”singură”, deoarece fiecare dintre celelalte cărți deja ocupă în acel moment locul corect.
Astfel, toate cărțile de pe raft au fost ordonate după înălțime (e mai logic că le ordonăm alfabetic, după autor, dar nu va fi vizibil rezultatul), dar numărul de permutări ale cărților va fi cu mult mai mic decât dacă am modela aranjarea acestora folosind algoritmul din lecția precedentă. Prin urmare, ne putem aștepta la o sortare mai rapidă în acest caz!

Descrierea algoritmului de selecție
Fie că avem un tablou a cu n elemente, având valorile: a[1], a[2],…, a[j], a[j+1], …, a[n].
Elementele de la a[1] până la a[j] încă nu sunt ordonate, în timp ce elementele a[j+1], …, a[n] formează un șir de valori ordonate crescător.
Mai mult, toate valorile elementelor a[1], a[2],…, a[j] nu depășesc valoarea elementului a[j+1].
Atunci, se parcurg toate valorile elementelor de la a[1] până la a[j] inclusiv, căutându-se printre ele elementul cu valoarea maximală. După se este determinat, acesta se schimbă cu locul cu elementul din poziția j : a[j].
Acum numărul elementelor neordonate s-a micșorat cu 1, în timp ce un element a fost ”așezat” în poziția corectă. Respectiv, se poate spune că j – indicele ultimului element încă neordonat, s-a micșorat cu 1!
Procedura descrisă se repetă până când numărul j al elementelor încă neordonate nu va deveni egal cu 1.
Evident, la începutul algoritmului se consideră că j are valoarea n – toate elementele din tablou formează fragmentul neordonat, în timp ce fragmentul ordonat nu conține nici un element.
Mai strict, algoritmul este descris pe pași în felul următor:
Pas 1. j ⟵n
Pas 2. Dacă j > 1 trecem la Pas 3, altfel trecem la Pas 6
Pas 3.max ⟵a[1], pmax ⟵1
Pas 4. Pentru toți i de la 1 la j verificăm
dacă a[i] > max atunci max ⟵a[i], pmax ⟵i
Pas 5. Schimbăm cu locul a[j], a[pmax], j ⟵j – 1, revenim la Pas 2
Pas 6. STOP, valorile din tabloul a au fost ordonate ascendent.
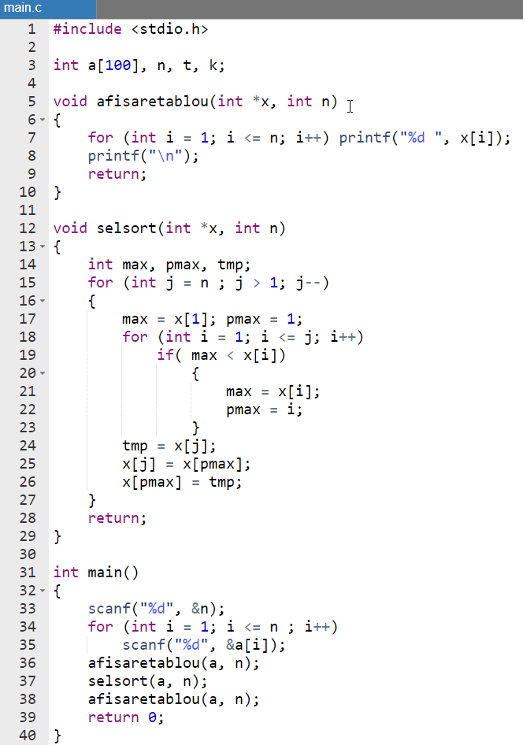
Tradițional includem librăria pentru citirea și afișarea datelor (linia 1), declarăm variabilele (linia 3).
Urmează descrierea funcției de afișare a tabloului, (liniile 5 – 10) care primește în calitate de parametru adresa tabloului de afișat și numărul curent de elemente în tablou.
Elementul principal al programuli este funcția care modelează algoritmul de sortare prin selecție – selsort (liniile 12 – 29)
Linia 15 – modelează modificarea numărului de elemente j în fragmentul încă nesortat – de la n la 1. Instrucțiunile subordonate inițializează elementul cu valoarea maximală și poziția lui (linia 17), caută elementul cu valoare maximală între elementele cu indicii cuprinși între 1 și j (exact acele elemente care formează fragmentul încă nesortat) (liniile 18 – 23), schimbă cu locul elementul cu valoare maximală cu ultimul dintre elementele din fragmentul nesortat (liniile 24 -26)
Funcția main are o structură clasică: citește datele inițiale (liniile 33 – 35), afișează elementele tabloului până la sortare (linia 36), apelează funcția de sortare prin selecție selsort (linia 37) și afișează repetat elementele tabloului după sortare (linia 38).
